ray's 16/32 bit atari page

downloads/misc

  demos/intros
  wolfenstein 3d
  miscellaneous
  bundeswehr

docs

  unrolling loops
  c2p part I (st)
  c2p part II (st)
  avoiding c2p (st)
  interlacing (st)
  fat mapping
  3d pipeline
  portal rendering
  8bpp color mixing
  fixedpoint math
  blitter (mst/ste)
  sample replay (st)
  blitter gouraud (falc)
  blitter fading (falc)
  arbitrary mapping
  frustrum clipping etc.

sourcecode

  mc68000 math lib
  32 bytes sin-gen
  24 bit tga-viewer
  blitter example
  lz77 packer
  lz78 packer
  protracker replayer

low demand frusctrum culling, fast triangle-clipping in 2d space effient facesorting and misc. topics

i'm having some leisure time over here at milliways 2k5 in kradd/.tscc.'s place so i decided to write another coding gem hopefully helpful to one or another.

so what's it gonna be about? at the time i wrote the 3d engine used in our eil entry 'beams' (sorry for the delay once again) sometime back in 2001 i had to come up with some ideas on how to perform fast triangle clipping in view-space and fast frustrum culling for the large screens that had a high face-count. now, the engine used in 'beams' is by no means optimized as can be, but however, many many sophisticated methods to perform the mentioned tasks are already known nowadays, some of which even found their way in hardware implementations. thus i decided to share a bit of experience i gathered while writing my engine in order to give a little advice in choosing from the palette of algorithms to those of you who are yet faced with the task of coding their own engine on a 'low-tech' system like the 16/32bit range of atari machines.

let me start off with the topic of sorting your geometry's faces which is required if you aim to achieve a correct visual result before rendering them into the screen (i.e. they have to be drawn in back to front order a method commonly referred to as the 'painter's algorithm') there are dozens of superior algorithms like the z-buffer (mostly found in hardware solutions and not reasonable on any atari due to its high demand), or the s-buffer, bsp-trees and other solutions that do not suffer from problems like rendering errors on cyclic overlapping faces unlike the painter's algorithm for instance but in which the trade-off between implementation effort and speed gain doesn't pay off imho (especially in using 68k assembler as a language).

so i decided to go for a plain face depth-sorting method which of course requires your sorting to be as quick as possible so of course you wouldn't go for any worst case o(n^2) algorithms like bubble-, selection sort or alike things. e.g. quick-sort is able to perform with o(n*log n) complexity in its best case but there is however another simple method which requires o(n) to sort the given set of objects outperforming quick-sort even with relatively low face counts (few hundreds of below) when realized carefully, namely the 'radix sort'. the idea of radix sort is basically to put your source array's entries into the appropriate places of a destination array of the same size according to a radix or key (in our case the face's depth) right away. at this point i would like to mention that it is generally recommended to use the average of the face's vertexes' z- coordinate as its depth and if your engine is limited to a constant vertex count (like 3 in my case) it's of course sufficient to only sum up these z-values without averaging.

normally it would take at least three passes to perform the task of sorting your array which are 1st: counting the radixes of a single class for all classes, meaning counting all faces of the same depth, 2nd: summing up the obtained values in order to transform them into indexes into the destination array and 3rd: using those indexes to put the source elements into the proper positions in the destination array.

using an array of linked lists as a destination array you can even omit the first two passes and put your source arrays faces into the proper position of the destination array, which i call the 'render queue'. if you aim at beating o(n*log n) type sorting algorithms (and of course you do ;) you'll have to reduce the solution's constant timing amount which gets mainly determined by the number of different classes. this means that we have to keep our z-granularity as coarse as possible but fine enough to still make a visual result that is free of glitches. i've found reserving 9 bits for the z-resolution to fulfil this demand. here comes some pseudo code to clarify the idea:

// data class definitions ZGRANULAR = 9 // bits for the depth resolution ZCLASSES = 1<<ZGRANULAR; typedef struct { ... int normal_z; // z coordinate of the face's normal int z; // the face's 'depth' } face_t; face_t face[NUMFACES]; // face mesh face_t * renderQueue[ZCLASSES] = { NIL }; // visibility list // sorting pass for (int n=0;n<NUMFACES;n++) { if (face[n].normal_z>0) { // add face to the destination list if it is facing us face[n].next = renderQueue[face[n].z]; renderQueue[face[n].z] = &face[n]; } } // rendering pass (back to front) for (int z=ZCLASSE-1;z!=0;z--) { while(renderQueue[z] != null) { // render faces with current depth renderface(renderQueue[z]); renderQueue[z] = renderQueue[z]->next; // next face } }

i hope you get the idea. the next paragraphs deal with the topic of discardable faces falling outside of your viewing frustrum (a cube in which segments of your geometry will be visible in our case) which is feasible when it comes to rendering scenes with many polygons some of which are probably completely or partly invisible.

culling faces that trivially fall completely into the space in the front of and behind of your viewing frustrum can be done with very low demand by extending the 2nd pass of the sort introduced above. imagine you'd first of all cut out a vertical slice of z-space directly in front of the viewer's omitting all faces that fall outside.

here comes the extension:

// vertex type typedef struct { int x,y,z ; // original coordinates int tx,ty,tz; // transformed coodinates ... // additional info... } vertx_t // vertex array vertx_t vertx[NUMVERTEXES]; ZMIN = 0; ZMAX = ZCLASSES; // sorting pass, leaving faces outside z-space for (int n=0;n<NUMFACES;n++) { if (face[n].normal_z>0 && vertx[face[n].vertex1].tz>ZMIN && vertx[face[n].vertex1].tz<ZMAX && vertx[face[n].vertex2].tz>ZMIN && vertx[face[n].vertex2].tz<ZMAX && vertx[face[n].vertex3].tz>ZMIN && vertx[face[n].vertex3].tz<ZMAX ) { // add face to the destination list if it is visible face[n].next = renderQueue[face[n].z]; renderQueue[face[n].z] = &face[n]; } }

with the convention met above (ZMIN=0 and ZMAX=ZCLASSE) it's possible to rescale your z-coordinates to maintain even more visual accuracy. you will now have culled trivial cases falling completely outside your z-space but what about the ones which are only partly outside?

well, concerning the z-clipping there's a quick and dirty but yet very effective solution that produces reasonable visual results: i.e. saturate your vertexes' z-value to the range of (ZMIN,ZMAX) prior to transforming from object into screen-space but save the non-clipped coordinate for the sorting pass, nonetheless. check it out, it looks ok. pseudo code ahead:

ZSCALE = 8 for (int n=0;n<NUMVERTEXES;n++) { // transform vertexes, assume (tx,ty,tz) // to hold your transformed vertex ... vertex[n].z = tz; // clamp the z-value if (tz > ZMAX) tz = ZMAX; if (tz < ZMIN) tz = ZMIN; // translate into screenspace vertex[n].x = (tx << ZSCALE) / tz; vertex[n].y = (ty << ZSCALE) / tz; }

ok, let's change to the next topic, clipping triangles obscured by the frustrum's horizontal and vertical boundaries. this can be performed in screen space. although it seems decent to keep as much calculus in registers as possible when for instance performing a time-critical action like rasterization, i reached the conclusion that using an edge-buffer in the rasterizer's scan-convertor has many advantages when it comes to clipping your triangles (or polygons of higher vertex count). it seems to run a bit off-topic now but you'll see what i'm aiming at later on. let me introduce a hint at the line clipping algorithm developed by cohen and sutherland. it subdivides screen-space into 9 areas assigned with the following bit-codes: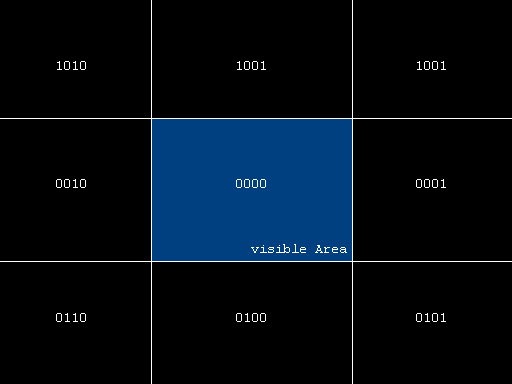

each of the bitfield's four flags has a certain meaning regarding the placement of each vertex (with '0000' meaning 'completely inside', bit #0: outside the right border, bit #1: outside the left border, bit #2: below the bottom border, bit #3: above the top border). maintaining a clipping code for each vertex after translation into view space has obvious advantages when it comes to sorting out non-trivial and trivial clipping cases, as you may read on. ahead of everything we will try to use these so called 'cohen-sutherland' clipping codes' to reject trivial cases that have all vertexes outside a certain screen boundary, thus falling out of the view-frustrum completely. this can be achieved by looking at bits each of the (three) vertexes have in common, i.e. check if their clipping code's logical and is different from zero. this will mark a trivial case so the face can be culled. pseudo code:

// extended vertex type typedef struct { int x,y,z; // original coordinates int x,ty,tz; // transformed coodinates char cs_code; // clipping flags ... // additional info... } vertx_t // sorting pass, expanded to reject trivial cases from the viewing frustrum // we assume the vertex clipping codes have already been computed before // (during your coordinate transform loop for instance) for (int n=0;n<NUMFACES;n++) { // sort out the trivial cases if (face[n].normal_z>0 && vertx[face[n].vertex1].tz>ZMIN && vertx[face[n].vertex1].tz<ZMAX && vertx[face[n].vertex2].tz>ZMIN && vertx[face[n].vertex2].tz<ZMAX && vertx[face[n].vertex3].tz>ZMIN && vertx[face[n].vertex3].tz<ZMAX && (vertx[face[n].vertex1].cs_code & vertx[face[n].vertex2].cs_code & vertx[face[n].vertex3].cs_code) == 0 ) { // add face to the destination list if it is visible face[n].next = renderQueue[face[n].z]; renderQueue[face[n].z] = &face[n]; } }

still with me so far? since now it's time to get slightly more complicated: non trivial cases and partly triangle clamping in 2d space. here you will see why it makes sense to use an edge- buffer; i will start with vertical clamping. this is easy: as you might know each triangle (face) section (i.e. edge) will be scan-converted separately. it's a common method to use two edge- buffers (one for the 'left' and one for 'right' face sections) directly obtaining the offset and length for each scanline to be rasterized. whether a section is to be placed into the left or right buffer is easy with triangles once you've vertically sorted the triangle's vertexes, i.e. just compute the 'direction' of the longest row of the triangle to select between one of the two possible configurations (2nd vertex to the left or 2nd vertex to the right of the triangle).

ok, back to the topic of vertical clamping. imagine a section to be scan-converted, call its vertexes v1 and v2 and assume those to be vertically sorted, with clipping codes already assigned, of course (as you probably remember bits #3 and #2 of the clipping codes will inform you about vertical boundary penetrations), there are 6 out of 16 possible situations: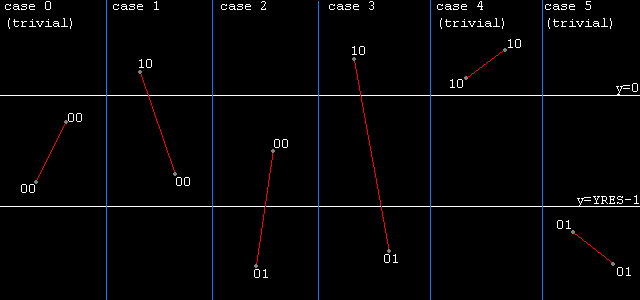

packing the clip-codes into a four bit field as above you can instantly use the codes as indexes into 16 entry jump-table pointing to 6 routines that do either trivially accept (case #1), omit (cases #5, #6) or clamp (cases #2, #3, #4) the given edge.

be careful when it comes to vertically clipping the triangle's longer edge, its clipped height will give you the possibly new number of visible scanlines that need to be rasterized, take this into account to set up your scanline loop counter.

once you have cut off invisible vertical parts you can once again use a jump-table for the 6 different horizontal setups (which are basically the same as the vertical possibilities). this time, however, you do not need to completely reject the edge-parts that fall outside of the frustrum but rather set those slices to the minimum/maximum horizontal coordinate along their vertical height depending on where which boundary is being crossed. and of course use bits #1 and #0 of the accordant clip- codes this time.

i think you get the idea, the nice thing about it: piss-easy implementation the main deal will be writing the loop setups for 2*6 cases in your scan-conversion routine and you don't even need to change your rasterization loop, at all. another advantage, it's also very easy to extend the method to different rasterization methods (lightning, texture-mapping etc.). a minor disadvantage, the method will leave out few trivial rejection cases and render those into clipped cases which will however be clamped off vertically or horizontally, respectively, thus costing some unnecessary bus transfers.

- 2005 ray//.tscc. -